Welcome back to another capsule on the (in)famous rocket equation. In the last one, we explored the general idea behind this and analyzed it in a vacuum. Thanks to that approach, we got a grasp on how to use this equation for a rocket that is traveling through space. But what about the launch phase? How does the rocket equation work for a rocket escaping Earth’s gravitational pull? It is time to find out and get one step further into the science and math of space travel.
Subheading IV: A New Force
Now, technically, the last capsule had more than three subheadings. However! It only had three “main” subheadings. And when dealing with a space-related topic, how could I pass up the chance to pay homage to the best space-centered franchise ever, Star Wars?
Anyway, the title for this section is not just a homage, it is accurate too. The main difference between this and the previous part of this duology of technical capsules is the presence of Earth’s gravitational field. Technically, even in space there would be some influence from nearby planets, stars, etc. and their gravitational fields; however, due to the relatively small impact they provide, doing a general calculation without including them still works to convey the math behind a rocket moving through space.
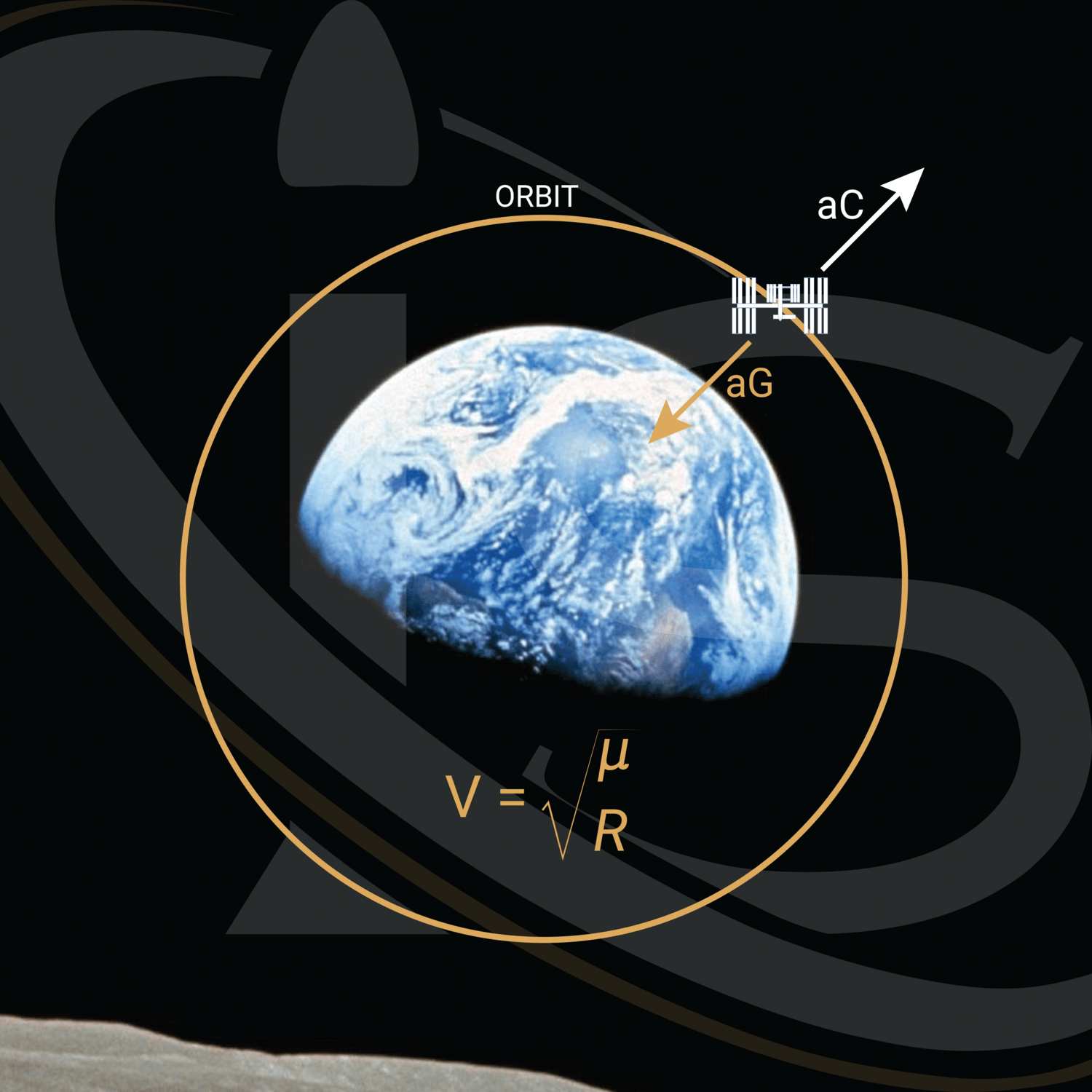
Going back to the topic at hand, though, Earth’s gravitational field is unescapable when it comes to a rocket leaving our planet. And yes, that was a very clever pun — if I do say so myself —based around how the whole purpose of today’s topic is to show the way rockets escape Earth’s pull. In terms of the actual math, however, the presence of Earth’s gravity can be described as follows:
![\[\vec{F} = -{m}{g}\hat{i}\]](https://impulso.space/wp-content/ql-cache/quicklatex.com-a8f379988381f13b3708806ed0844696_l3.png "Rendered by QuickLaTeX.com")
The reason for the negative sign is quite simple. The rocket’s trajectory is (basically) along the exact opposite direction of Earth’s gravitational field. It is trying to leave Earth, after all.
Some Physics Required
Before going any further, it is important to establish the general relationship between force and momentum:
![\[\vec{F}({t}) = \frac{{d}{\vec{p}}}{dt}\]](https://impulso.space/wp-content/ql-cache/quicklatex.com-9bb210b891e32a3f7f7664d9a5ee6724_l3.png "Rendered by QuickLaTeX.com")
In this case, we can take this concept one step further and talk about the impulse, which is both equal to the change in momentum and given by the following:
![\[d\vec{J} = \vec{F}{dt} = -mgdt\hat{i}\]](https://impulso.space/wp-content/ql-cache/quicklatex.com-7d7cfc8a7a700707568e77f21b1ced6b_l3.png "Rendered by QuickLaTeX.com")
Therefore, we can combine all of the concepts above into one equation:
![\[\vec{p}_{f} - \vec{p}_{0} = -mgdt\hat{i}\]](https://impulso.space/wp-content/ql-cache/quicklatex.com-f472158b179b2bac3c11c79c57d4b314_l3.png "Rendered by QuickLaTeX.com")
One quick physics/math note for anyone wondering. The reason the impulse derivative can be equated to the momentum — even though impulse is equal to the change in momentum — one has to do with how derivatives, themselves, work. These represent infinitesimal changes; so, a quantity equaling the finite change of another one does not mean that the former is a derivative of the latter. This is, relatively, common knowledge at higher level math, but it can be very confusing when it is first introduced.
Putting Gravity in the Rocket Equation
Now that we have the basic physics for the impulse and change in momentum that Earth’s gravity will produce, it is time to connect them to the rocket equation itself. I will not go over how we got to the momentum we will use below, but, for those who are curious, it is all explained here. Anyway, using the momentum for the rocket and exhaust gas, we get the following equation:
![\[[{(m - dm_{g})}{(v + dv)} + {dm_{g}}{(v - u)} - mv]\hat{i} = -mgdt\hat{i}\]](https://impulso.space/wp-content/ql-cache/quicklatex.com-8287405f49d0442cb2fc4e638e942bcf_l3.png "Rendered by QuickLaTeX.com")
Just like last time, the equation can be simplified by taking out the dmgdv term, since that is two infinitesimals multiplied together. Furthermore, we can change dmg to -dm, because the change in mass of the rocket must be equal and opposite to that of the exhaust gas. This yields:
![\[mdv = -dmu - mgdt\]](https://impulso.space/wp-content/ql-cache/quicklatex.com-42970f46ab7772be5477419f052410cc_l3.png "Rendered by QuickLaTeX.com")
Integrals As Far As the Eye Can See
All that is left to do now is solve the equation above. And as this is another equation of infinitesimals, the hero of math will come to the rescue once again. It is time to use the integral! Although, this time there will be three separate integrals, as there is a new term that was not present in the first part. Regardless, it is time to get the rocket equation for a spacecraft leaving Earth.
![\[\int_{v_{0}}^{v}dv = -u\int_{m_{0}}^{m} \frac{dm}{m} - g\int_{t_{0}}^{t}dt \longrightarrow {\Delta}{v} = {u}{ln(\frac{m_{0}}{m}) - g\Delta{t}\]](https://impulso.space/wp-content/ql-cache/quicklatex.com-c087303af908711cf113d7b98264920f_l3.png "Rendered by QuickLaTeX.com")
This should look familiar to anyone who read the first part. Which by the way, if you got this far and still have not checked out part 1, go do that right now. I will even link it again here. Seriously, unless you already know this equation — if that is you, thank you for still choosing to check out this capsule — none of what I said today will make any sense without the background information provided in part 1. Anyway, the equation above is basically the same as the one for the rocket equation in space. With one key difference, that is. The presence of gravity will affect the velocity of the rocket.
What Does This Tell Us?
There are a couple of things to point out when it comes to the differences for the rocket equation with and without outside forces. For one, the velocity for the rocket will be increasing more slowly. This makes sense, of course, as Earth’s gravity is constantly counteracting the force generated by burning the rocket’s propellant.
However, there is something else that is worth mentioning. In the first rocket equation that we discussed, there was no time component. That meant that no matter how long it would take, a change in mass would always lead to the same change in velocity. But that is not the case with the second equation. With the addition of an external force, such as gravity, the rocket’s change in velocity will be inversely affected by the passing of time. Therefore, the quicker the time span needed for the fuel to be burned, the more efficient the whole process will be.
In other words, when a rocket is taking off, one of the most crucial aspects is how fast can it accelerate. This is why liftoff involves an “explosion” of sorts, as that is the effect of trying to burn the propellant as quickly as possible.
And to reiterate this point one more time, even when a rocket is in space, there will still be some outside force present. Therefore, the second version of the equation is, technically, the most complete one, as it accounts for all factors. However, with the massive amount of force generated by a rocket’s engine, something like the gravitational pull of a planet that is thousands of kilometers away will not impact its velocity too greatly.
Using The Rocket Equation
As I said last time, I have the general plan of using this equation to get a more accurate estimate of the energy used in the Artemis I mission. However, I still need to study up on some other topics before I can do that. In the meantime, if you would like to see concrete examples of how to use this, let us know in the chatbox and we will work on a technical capsule just for that. Next week is back to the science capsules, though, with the final Galilean Moon, Europa, taking center stage. This is possibly the object most likely to have the conditions to host life outside of Earth! So make sure to come back here, at impulso.space, next Wednesday, because you will not want to miss that.
