What Exactly Are the Forces that Act Upon a Satellite?

As with any object that is not located in a vacuum with no external forces acting on it whatsoever, satellites constantly experience a multitude of forces while out in space. Of course, the most obvious force acting on a satellite is that due to Earth’s gravitational field; however, that is only one of many forces present. The other major ones include: the gravitational fields of other celestial bodies, mainly the Sun and the Moon, and solar radiation pressure.

Let us start off by talking about the various gravitational forces experienced by a satellite. First, we should define the equation for the gravitational force acting on any given object due to the presence of a second one. That being:

   

Where:

F = force due to gravity;

G = gravitational constant;

m₁  and m₂ = masses of the two objects;

r = distance between the two objects.

Looking at this equation, we can see that the distance between the two objects will be the greatest determining factor for the magnitude of the gravitational force, as that quantity is squared, meaning that any change to it will impact the equation exponentially. This is also the reason why the force from Earth’s gravitational field will have a greater impact on the satellite than that of the force from the Sun’s gravitational field, even though the Sun is much more massive than the Earth. It then follows that the Moon, being both further from the satellite and less massive than the Earth, would have an even lesser impact on the overall gravitational force experience by the satellite. 

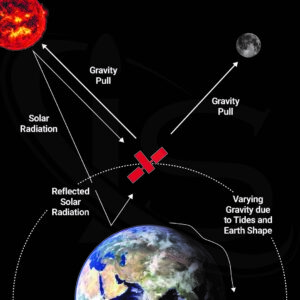
Just to put this in perspective, let us take a look at the numbers for the satellite type that will be further from Earth, the GEO satellite, sitting at a distance of about 35,786 km (or 22,236 mi). Using a relatively average satellite weight of 3,000 kg, the masses of each celestial body, and an average distance from the Sun and Moon of 148,270,400 km and 384,440 km, respectively, we get the following gravitational forces:

F_E = 672.18 N

F_S = 17.52 N

F_M = 0.099 N

Note: The value used for r was the distance from the celestial body to the satellite plus the radius of said celestial body. I.e. for Earth:

r_E = 35,786,000 m + 6,378,000 m = 42,164,000 m

This shows how the Earth exerts by far the most dominant force on the satellite, with the Sun being a somewhat distant second, and the moon an even more distant third. Keep in mind that the calculations here were done with the satellite type located furthest from Earth, the GEO, which means that a MEO or LEO satellite would experience an even greater influence from Earth’s gravitational pull.

Moving on to solar radiation pressure, and it is important to first define what exactly radiation pressure is. The starting point for this concept lies with momentum. Any object in motion has, by definition, momentum, and this includes electromagnetic waves as well. These waves, in the case of solar radiation pressure, are what is intended when talking about the radiation emanating from the Sun. As they make their way through space, it is inevitable that they will eventually collide with some object on their path, whether that be a planet, an asteroid, or, for our purposes, a satellite. When these collisions happen, a transfer of momentum and, therefore, energy occurs, much like it would with any classical collision between two solid objects. The only difference here, is that the change is caused by the interaction of an object with an electromagnetic field of waves, as opposed to something like a ball being hit by a tennis racket.

To get the actual change in momentum, some math needs to be done, including figuring out just how much momentum the waves themselves are carrying. This is where the concept of radiation pressure comes in. After all, pressure is defined as Force/Area, and force is just the derivative of momentum with respect to time, meaning that all these quantities are intrinsically connected. In fact, the idea of waves carrying momentum, first theorized by Maxwell in 1862, is what gave rise to the concept radiation pressure. 

The math for the full derivation of radiation pressure is a bit involved; fortunately, we do not need to go through all of that today, as we are simply interested in how solar radiation pressure can affect satellites (you are more than welcome to look this up, however, if you are someone like me who is quite fond of math.) For this end, the two equations needed to understand the basics are the following:

Where:

P = radiation pressure

I = intensity of the wave

c = speed of light

As satellites are neither perfectly reflective nor opaque, the equation needed to figure this out will be one that is somewhere in the middle of the two above. This will change for each satellite, as not all satellites are exactly the same; still, there are some concrete examples online that give a specific answer for a certain satellite. One such example I found is the following from the Science.org website: For a 12-foot Beacon satellite located about 1600 km above the Earth, the orbit can be changed by a rate of up to 1.12 km per day (about 0.07%) due to solar radiation pressure. This serves a good indicator of the pretty sizable effect that this phenomenon can have on a satellite.

Before we conclude, it is also important to point out that there are other less prevalent forces acting on satellites, such as those due to the gravitational pulls of nearby planets. However, their effect is not felt as much as that of the ones we discussed today.